week10 lec2#
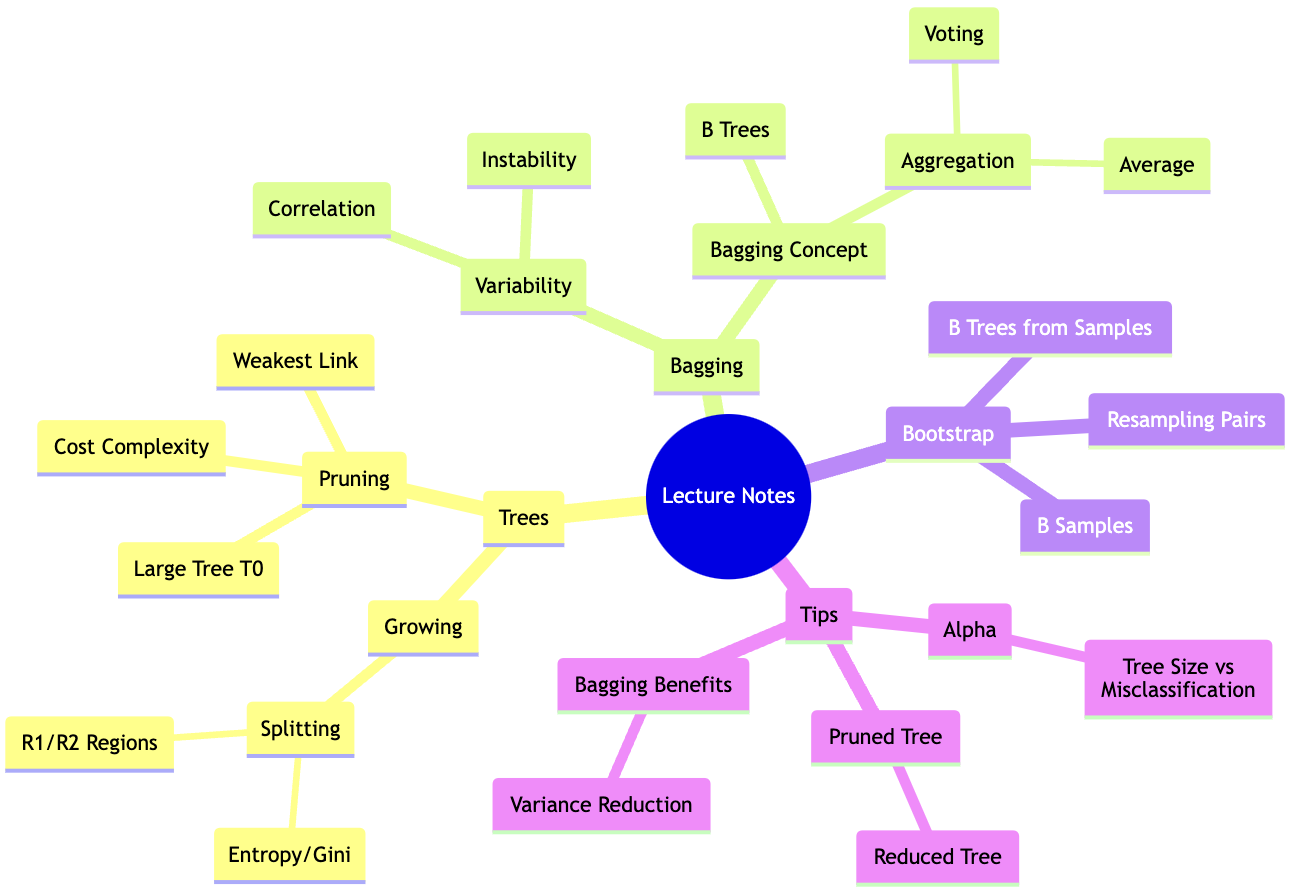
Lecture Notes: Decision Trees and Bagging
1. Growing the Tree
Objective: Construct a decision tree by splitting data into regions based on predictor variables.
Entropy/Gini Index: Denoted as \( Qℓ \). Used to measure the impurity of a node.
Steps:
Possible Splits: Consider all ways to split data into two regions \( R1 \) and \( R2 \) based on predictor values.
First Tree Creation: Choose the splitting variable and point that minimizes \( \sum_{ℓ=1}^{2} NℓQℓ \).
Subsequent Splits: Repeat the procedure on the newly created regions.
Tip: The goal is to minimize impurity in each region.
2. Pruning the Tree
Objective: Simplify a large tree to avoid overfitting.
Initial Tree: Grow a large tree \( T0 \) such that each region contains a small number of observations.
Cost Complexity Criterion: Used to prune the tree. Defined as \( Cα(T) = \sum_{l=1}^{|T|} NlQl(T) + α|T| \).
Weakest Link Pruning:
Collapse nodes that result in the smallest increase in \( \sum_{l=1}^{|T|} NlQl(T) \).
Repeat until a single leaf tree remains.
Compute \( Cα(T) \) for all trees in the sequence.
Tip: \( α \) is chosen by cross-validation. It balances tree size and fit to the data.
3. Bagging Classification Trees
Objective: Reduce the variance of decision trees.
Problem with Trees: High variability. Similar samples can produce different trees.
Solution: Bagging. Produce multiple trees and aggregate them.
Deep Trees: Have small bias but large variance. Aggregating reduces variance.
Tip: Bagging helps stabilize predictions, especially when predictor variables are correlated.
4. Bootstrap Samples
Objective: Create multiple artificial samples from the original data.
Bootstrap Procedure: Draw randomly with replacement to create new samples.
Bootstrap Sample: Each artificial sample. Denoted as \( (X∗b,1, G∗b,1), . . . , (X∗b,n, G∗b,n) \).
Tip: Resampling is done for pairs, not individual values.
5. Aggregating Trees in Bagging
Objective: Combine predictions from multiple trees.
Methods:
Majority Voting: Classify based on the class with the highest proportion across trees.
Averaging Class Proportions: Calculate average class proportions for each tree and classify based on the highest average.
Tip: Averaging class proportions tends to work better, especially for small numbers of trees.
6. Real-world Application: Spam Classification
Data: Information from 4601 emails. Predictors are relative frequencies of common words/punctuation.
Goal: Predict if an email is spam or genuine.
Results: Confusion matrix showed an error rate of 9.3%. The classifier performed reasonably well, with a small misclassification rate.
Key Takeaways:
Decision trees are powerful but can be highly variable.
Pruning and bagging are techniques to enhance the performance of trees.
Bootstrap samples are essential for bagging, allowing the creation of multiple trees.
Aggregation methods, like majority voting and averaging, help in consolidating predictions from multiple trees.